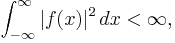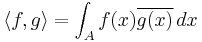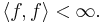Square-integrable function

In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite. Thus, if

$\int_{-\infty}^\infty |f(x)|^2 \, dx < \infty,$

then ƒ is quadratically integrable on the real line (−∞, ∞). One may also speak of quadratic integrability over bounded intervals such as [0, 1].

The quadratically integrable functions form an inner product space whose inner product is given by

$\langle f, g \rangle = \int_A f(x) \overline{g(x)} \, dx$

where

g(x) is the complex conjugate of g,
A is the set over which one integrates—in the first example above, A is (−∞, ∞); in the second, A is [0, 1].

Since |a|² = a a, quadratic integrability is the same as saying

$\langle f, f \rangle < \infty. \,$

It can be shown that quadratically integrable functions form a complete metric space, hence a Banach space. As we have the additional property of the inner product, this is specifically a Hilbert space. This inner product space is conventionally denoted L².

The space of quadratically integrable functions is the L^p space in which p = 2.